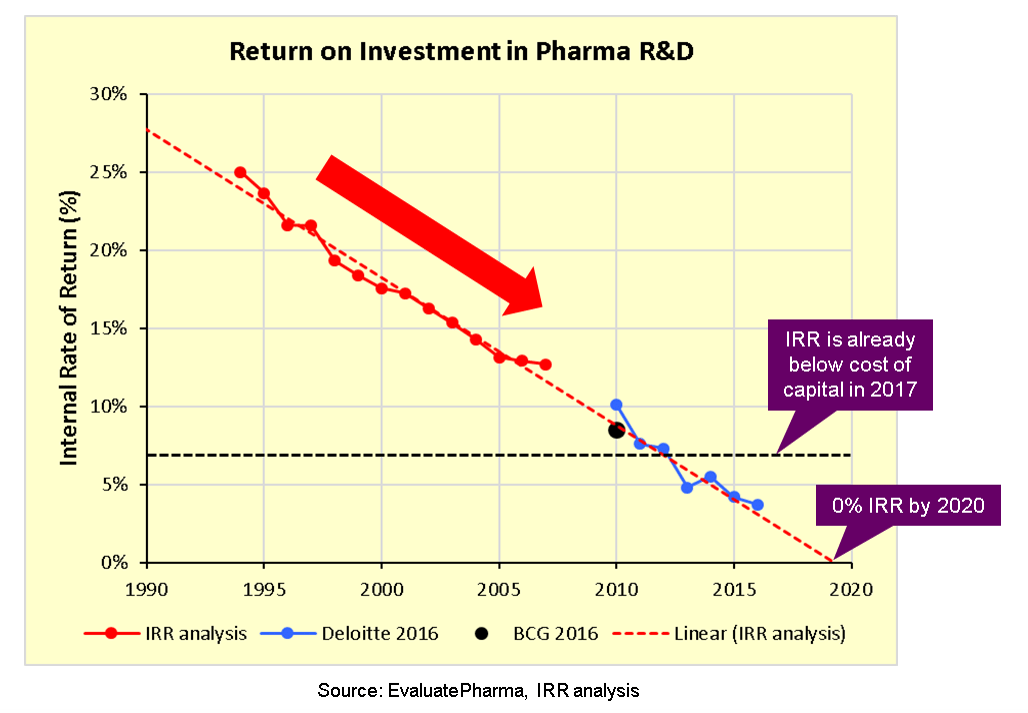
Pharma's broken business model: An industry on the brink of terminal decline
Biotech Voices is a collection of exclusive opinion editorials from some of the leading voices in biopharma on the biggest industry questions today.
Biotech Voices is a contributed article from select Endpoints News readers. Commentator Kelvin Stott regularly …
Sign up to read this article for free.
Get free access to a limited number of articles, plus choose newsletters to get straight to your inbox.